As you know if you’ve been following these things, this crew have gotten their “Inner Ross Perot” on and given us a “This is what Health Care Reform looks like” (as opposed to their bubble-plague graphs which have been ripe for mockery):

Health Care Reform looks roughly like this, they say:

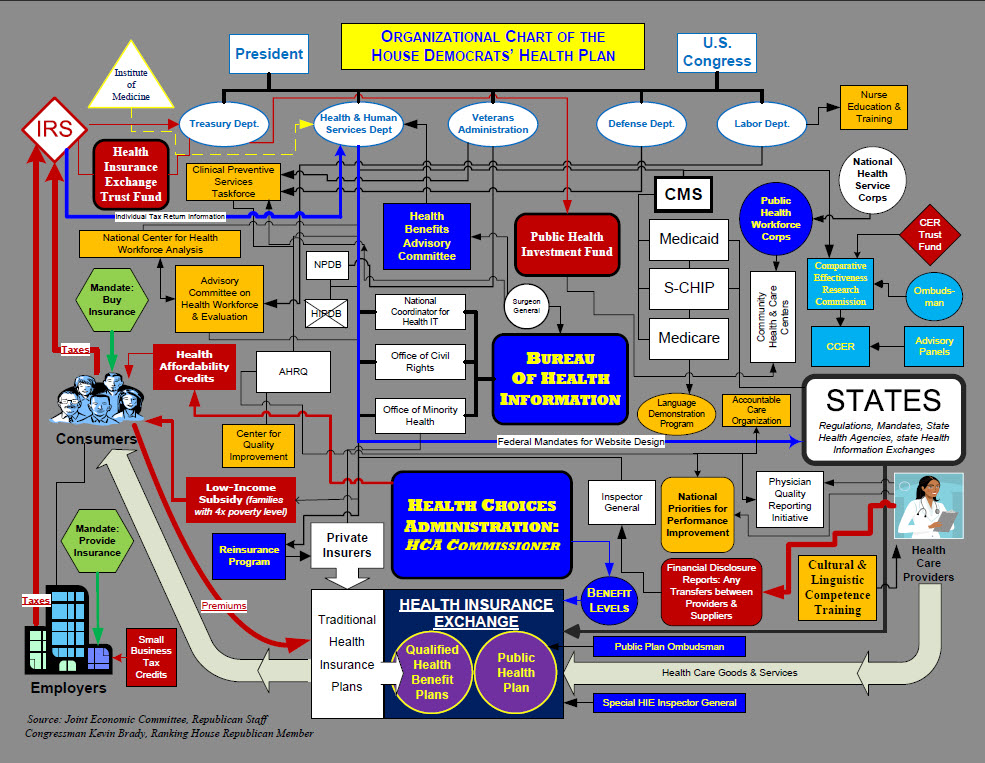
It is a design that obfuscates more than it illuminates, an attempt at the 1994 graph used by Bob Dole to show a bunch of bureacracies getting in between you and your doctor.  I recall Conan O’brien having Bob Dole on his program, and having a gag with him where he questioned the honesty of the graph by “zooming in” to one of the boxes to show one of the new bureacracies as “The National Basketball Association”.

Or… I have engaged in some form of “Create instructions for simple task”s exercise on more than one occasion.  “Make a Peanut and Belly Jelly Sandwich”, for instance.  Or better still for my illustration:  “Here’s a fairly simple design of boxes and circles.  Write up instructions on how to draw them.”  When given this type of exercise, my inclination is to create a precisely correct, but purposefully difficult to comprehend unless the listener is paying close attention, instructions.  It’s a project where I’d want it to end up where the person following the instructions will screw up, but I will be certain that it would be his/her fault. 

The New Republic rebuts this chart, in part with a chart of our current system.:

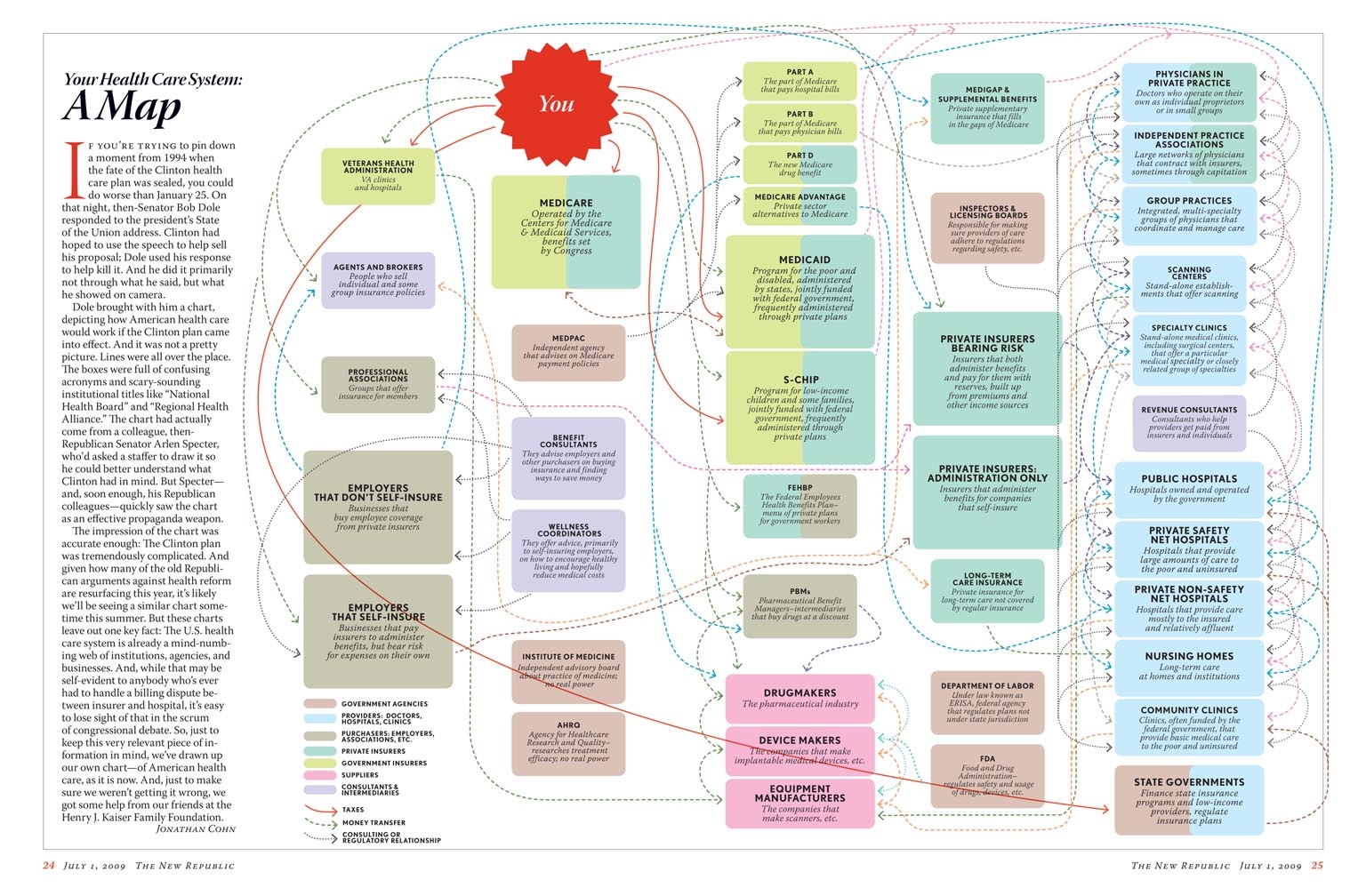
The graph is, I would say, a lot more honest — illuminates more than it obfuscates.  In the end, a lot of the arguments against is striking me as arguing that we’re just replacing one box with another — sympathetic supposition, I suppose, particularly as Congress and the Obama Administration are hammering out what amounts to the compromise of a compromise of a compromise of a compromise.

A clearer cut chart can be drawn for this piece of legislation.  Something to the effect of a Vinn Diagram — Humans on one side, Animals on the other, with a giant “NO!!!” in the point where the two circles meet.

This entry was posted on Sunday, July 26th, 2009 at 1:48 pm and is filed under Uncategorized. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.